Γεωμετρικά σχήματα, ή τι αρχίζει η γεωμετρία;

Πολλοί άνθρωποι πιστεύουν λανθασμένα ότι για πρώτη φοράσυναντούν γεωμετρικά στοιχεία στο γυμνάσιο. Εκεί μελετούν τα ονόματα, τις ιδιότητες και τους τύπους τους. Αλλά στην πραγματικότητα, από την ίδια την παιδική ηλικία, κάθε αντικείμενο που το παιδί βλέπει, αισθάνεται, μυρίζει ή αλληλεπιδρά με αυτό με οποιονδήποτε άλλο τρόπο, είναι ακριβώς μια γεωμετρική μορφή. Ο καναπές στον οποίο βρίσκεται η νεογέννητη γυναίκα - ένα ορθογώνιο, ένας λαμπτήρας, που δίνει στους μαιευτήρες ένα φως - μια στρογγυλή φιγούρα, παράθυρα στα παράθυρα - πλατείες. Ο κατάλογος αυτός μπορεί να συνεχιστεί επ 'αόριστον.

Γεωμετρικά σχήματα, απευθείας ωςτο στοιχείο της επιστήμης, αντιμετωπίζεται για πρώτη φορά από τους μαθητές των μεσαίων τάξεων. Μπορείτε ακόμη να πείτε ότι η γεωμετρία αρχίζει μαζί τους. Ωστόσο, όπως ήδη αναφέρθηκε παραπάνω, οι πρώτες αλληλεπιδράσεις μαζί τους συμβαίνουν πολύ πριν από αυτό. Πάρτε, για παράδειγμα, ένα σημείο. Είναι ο μικρότερος αριθμός στη γεωμετρία. Επιπλέον, θεωρείται ότι είναι η βάση όλων των υπόλοιπων (ως άτομα στη χημεία). Όλα τα τρίγωνα, τα τετράγωνα και άλλες μορφές σε οποιοδήποτε σχέδιο αποτελούνται από ένα σύνολο σημείων. Έχουν κάποιες ιδιότητες, κάθε μία από τις οποίες είναι εγγενής μόνο σε μία φιγούρα (κανένας άλλος δεν μπορεί να τους προικίσει).

Μπορούμε να υποθέσουμε ότι όλες οι γεωμετρικές μορφέςαποτελούνται άμεσα από γραμμές, αλλά τι είναι αυτό; Αυτό είναι το σύνολο των σημείων που είναι διατεταγμένα σε μια σειρά. Μπορούν να συνεχιστούν επ 'αόριστον, επειδή η ευθεία γραμμή δεν τελειώνει. Εάν οριοθετείται από δύο πλευρές, τότε ονομάζεται συνήθως τμήμα. Εάν υπάρχει μόνο ένας περιορισμός, τότε υπάρχει μια ακτίνα μπροστά σας. Συνεπώς, όλα τα επίπεδα στοιχεία στη γεωμετρία αποτελούνται από τμήματα, καθώς τα συστατικά έχουν τόσο τέλος όσο και αρχή. Θα πρέπει να σημειωθεί ότι η ευθεία, η οποία διαιρέθηκε από ένα σημείο, είναι δύο ακτίνες που κατευθύνονται προς αντίθετες πλευρές.

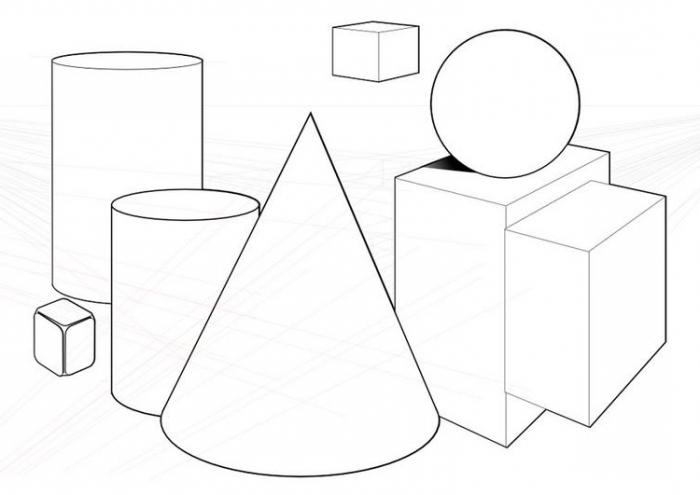
Όχι μόνο των επίπεδων στοιχείων είναι η γεωμετρία,υπάρχουν και τρισδιάστατα γεωμετρικά σχήματα. Για να τις μελετήσουν στο σχολείο αρχίζουν αργότερα, πιο κοντά στο τέλος των σπουδών τους, αλλά ένα πρόσωπο τους συναντά, και πάλι, πολύ νωρίτερα. Για παράδειγμα, όταν ένα παιδί παίρνει ένα κύβο στα χέρια του, κρατά ένα κύβο στα χέρια του. Ή, αν κοιτάξει το συρτάρι, τότε μπροστά του είναι ένα ορθογώνιο παραλληλεπίπεδο. Όλες οι τρισδιάστατες μορφές αποτελούνται από επίπεδα (δηλαδή, είναι μια απεριόριστη πρωτεύουσα έννοια, καθώς και μια ευθεία γραμμή). Το ίδιο παραλληλεπίπεδο αποτελείται από έξι τέτοια στοιχεία. Μπορείτε να δείτε οπτικά το αεροπλάνο κοιτάζοντας την επιφάνεια κάθε πίνακα. Αλλά αυτό θα είναι μόνο ένα μέρος της, αφού υπάρχουν περιορισμοί. Το ίδιο το αεροπλάνο είναι εξίσου άπειρο με την ευθεία γραμμή.

Έτσι, δεν υπάρχει σφαίρα όπου δεν συναντάμεγεωμετρικά σχήματα. Τα ονόματά τους είναι διαφορετικά, καθορίζουν τις ιδιότητες και τα χαρακτηριστικά. Για παράδειγμα, ο τύπος της περιοχής ενός τριγώνου δεν είναι κατάλληλος για ορθογώνιο ή τετράγωνο.

Είναι επιθυμητό να συνδέσετε το παιδί με γεωμετρικό τρόποστοιχεία από το νηπιαγωγείο. Μπορείτε να τα κάνετε μόνοι σας και στη συνέχεια να τα διανείρετε σε διαφορετικά σχέδια σε χαρτί (αν είναι επίπεδη στοιχεία). Ωστόσο, μην εγκαταλείπετε τις τρισδιάστατες μορφές. Στο Διαδίκτυο, μπορείτε να βρείτε πολλά διδακτικά παιχνίδια που σχετίζονται με αυτό. Αλλά δεν μπορείτε να αναβάλλετε τη γνωριμία με αυτά, γιατί όλα όσα βλέπουμε - γεωμετρικά σχήματα. Ακόμα και ένα άτομο αποτελείται από αυτά!