Βασικοί τύποι και παράδειγμα κυκλικών αλγορίθμων

Το άρθρο έχει σχεδιαστεί για να παρέχει βασικές έννοιες του τι είναι ένας κυκλικός αλγόριθμος, ο οποίος είναι κοινός σε οποιαδήποτε γλώσσα προγραμματισμού και στο επίπεδο προετοιμασίας του προγραμματιστή.

Η έννοια ενός αλγορίθμου

Ένας αλγόριθμος είναι μια ακολουθία ενεργειώνγια την επίλυση ενός υπολογιστικού και άλλου προβλήματος σε ένα πεπερασμένο αριθμό βημάτων. Οι ενέργειες (οδηγίες) για την εκτέλεση του αλγορίθμου μπορούν να εκτελούνται το ένα μετά το άλλο (διαδοχικά), ταυτόχρονα (παράλληλα) ή με αυθαίρετη σειρά, χρησιμοποιώντας κύκλους και συνθήκες μετάβασης. Οι αλγόριθμοι χρησιμοποιούνται όχι μόνο στον προγραμματισμό αλλά και σε άλλους τομείς δραστηριότητας, για παράδειγμα στη διαχείριση της παραγωγής και των επιχειρηματικών διαδικασιών.

Κυκλικοί αλγόριθμοι

Ένας αλγόριθμος λέγεται ότι είναι κυκλικός αν είναι σε αυτόΥπάρχουν ενέργειες ή ομάδες ενεργειών που πρέπει να εκτελεστούν περισσότερες από μία φορές. Επαναλαμβανόμενες αλγοριθμικές ενέργειες είναι το σώμα ενός κύκλου. Επιπλέον, κάθε κύκλος έχει μια προϋπόθεση ότι τελειώνει η εκτέλεση του κυκλικού αλγορίθμου.

Τύποι κυκλικών αλγορίθμων

Κάθε κυκλικός αλγόριθμος έχει στη σύνθεσή τουη συνθήκη του βρόχου, δηλαδή μια λογική έκφραση του οποίου το αποτέλεσμα καθορίζει εάν το σώμα βρόχου θα εκτελεστεί για μία ακόμη φορά ή ο βρόχος θα τερματιστεί. Με τη μέθοδο επεξεργασίας, όλοι οι κυκλικοί αλγόριθμοι χωρίζονται σε τρεις ομάδες.

Κύκλος με προϋπόθεση

Σε αυτούς τους κυκλικούς αλγορίθμους, η κατάσταση συνέχισης ελέγχεται πριν από την επεξεργασία του σώματος του βρόχου, δηλαδή, υπάρχει ανάγκη να επαναληφθεί η επεξεργασία του βρόχου.

Εξετάστε την έξοδο αριθμών από -5 έως 0 ως παράδειγμα κυκλικών αλγορίθμων με προϋπόθεση:

Στοιχεία του αλγορίθμου:

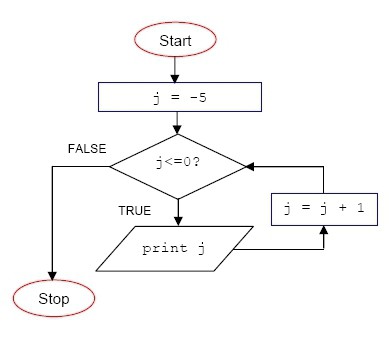
1. Ορίστε την αρχική τιμή της μεταβλητής βάσης j σε -5.
2. Ελέγουμε την κατάσταση του κύκλου. Η συνθήκη είναι θετική και το σώμα βρόχου εκτελείται για πρώτη φορά.
3. Στη συνέχεια προσθέτουμε 1 στη μεταβλητή j, ελέγξουμε ξανά την κατάσταση του κύκλου.
4. Ο βρόχος συνεχίζει να λειτουργεί όσο η τιμή του j είναι μικρότερη ή ίση με το μηδέν, διαφορετικά βγαίνουμε από τον βρόχο στον κλάδο FALSE

Κύκλος με μεταχρέωση

Ο έλεγχος κατάστασης εκτελείται μετά την πρώτη επεξεργασία του σώματος βρόχου και ελέγχει την έξοδο από αυτό.

Ας αναλύσουμε τον υπολογισμό του αθροίσματος από το 1 στον αριθμό n ως παράδειγμα κυκλικών αλγορίθμων στους οποίους χρησιμοποιείται η μεταχρέωση:

1. Εισάγουμε έναν πεπερασμένο αριθμό του υπολογισμού του άθρου n και θέτουμε μηδενικές αρχικές τιμές του συνολικού αθροίσματος αθροίσματος και του μετρητή του κύκλου i.
2. Ο βρόχος εκτελείται πριν από τον πρώτο έλεγχο της κατάστασης.
3. Ελέγουμε την κατάσταση του βρόχου, δηλαδή η τιμή του μετρητή i είναι μικρότερη ή ίση με n.
4. Εάν το αποτέλεσμα της κατάστασης είναι θετικό, εκτελούμε ξανά το βρόχο, διαφορετικά τερματίζουμε το βρόχο και εκτυπώνουμε το άθροισμα στην οθόνη ή εκτυπώνουμε.

Κύκλος άνευ όρων

Συνήθως χρησιμοποιείται σε αλγόριθμους όταν ο απαιτούμενος αριθμός εκτελέσεων βρόχου είναι γνωστός εκ των προτέρων και χρησιμοποιείται πολύ συχνά όταν εργάζεται με συστοιχίες.

Ένας τέτοιος αλγόριθμος περιέχει τρία υποχρεωτικά στοιχεία:

1. Η τιμή εκκίνησης, η οποία ονομάζεται παράμετρος βρόχου, επειδή αυτή η μεταβλητή αλλάζει μετά από κάθε εκτέλεση του κύκλου και καθορίζει το χρόνο ολοκλήρωσής της.
2. Η τιμή στην οποία τερματίζεται ο βρόχος.
3. Βήμα κύκλου.

Σε κάθε βήμα, το πρόγραμμα επαληθεύει αυτόΕάν η αρχική τιμή είναι πεπερασμένη. Και αν ναι, ο κύκλος τελειώνει. Διαφορετικά, προσθέτουμε το μέγεθος βήματος στην τιμή έναρξης και ο κύκλος επαναλαμβάνεται. Θα πρέπει να σημειωθεί ειδικά ότι οποιοσδήποτε άνευ όρων κύκλος μπορεί να αντικατασταθεί από έναν υπό όρους ένας με προ- ή μετα-προϋπόθεση.

Κατά την κατάρτιση κυκλικών αλγορίθμων,να τηρούν δύο υποχρεωτικές προϋποθέσεις. Πρώτον, για να τερματίσετε τον βρόχο, είναι απαραίτητο τα περιεχόμενα του σώματος να επηρεάσουν τη θέση ή την προϋπόθεση, διαφορετικά μπορούμε να καταλήξουμε με έναν άπειρο βρόχο. Αλλά για ορισμένες εργασίες λογισμικού εφαρμόζονται τέτοιοι κύκλοι. Ως παράδειγμα κυκλικών αλγορίθμων που λειτουργούν επ 'αόριστον, μπορούμε να αναφέρουμε το λειτουργικό σύστημα των Windows, όπου χρησιμοποιείται ένας άπειρος κύκλος δημοσκόπησης ποντικιών για τον προσδιορισμό των ενεργειών του χρήστη. Δεύτερον, οι μεταβλητές που μεταφέρονται στον βρόχο πρέπει να παρέχουν τουλάχιστον μία εκτέλεση.

Υπολογισμός του παράγοντα

Για να εδραιωθεί η ανάγνωση, δίνουμε ένα παράδειγμακυκλικούς αλγορίθμους για τον υπολογισμό του παράγοντα ενός ακέραιου αριθμού. Το παραπάνω παράδειγμα είναι ένας βρόχος με προϋπόθεση, αλλά είναι δυνατή η εφαρμογή κάθε είδους κυκλικού αλγορίθμου.

• Εισαγωγή: τα δεδομένα είναι ένας ακέραιος για τον οποίο ορίζεται ο παράγοντας.
• Μεταβλητές συστήματος: η παράμετρος του κύκλου i, η οποία λαμβάνει τιμές από 1 έως δεδομένα στο βήμα 1.
• Αποτέλεσμα: ο μεταβλητός παράγοντας είναι ο παράγοντας των αριθμητικών δεδομένων, το οποίο είναι το προϊόν των ακεραίων από 1 έως τα δεδομένα.

Εξετάστε τον αλγόριθμο με βήματα:

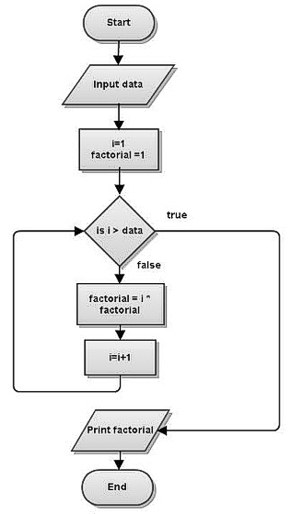
1. Ο αλγόριθμος έλαβε τα αριθμητικά δεδομένα, για τα οποία είναι απαραίτητο να υπολογίσει τον παράγοντα.
2. Ο μεταβλητός παράγοντας, στον οποίο θα αποθηκευτεί το τελικό αποτέλεσμα, έχει μια τιμή ενός.
3. Οργανώνουμε τον βρόχο με την παράμετρο i και την αρχική τιμή 1. Η τελική τιμή είναι τα αρχικά δεδομένα αριθμού. Μόλις η τιμή του μετρητή i είναι μεγαλύτερη, ο βρόχος τερματίζεται.
4. Ο κύκλος του υπολογιστικού παράγοντα εκτελείται - οι τρέχουσες τιμές του παράγοντα και του μετρητή i πολλαπλασιάζονται.
5. Στην τιμή του μετρητή προσθέστε μια μονάδα, ελέγξτε την κατάσταση του βρόχου και, εάν το αποτέλεσμα είναι θετικό, τερματίζουμε.
6. Μετά την τελευταία επανάληψη του βρόχου, η τιμή των παραγοντικών δεδομένων! παραμένει σε παράγοντα και εμφανίζεται ή εκτυπώνεται.

</ p>